Research

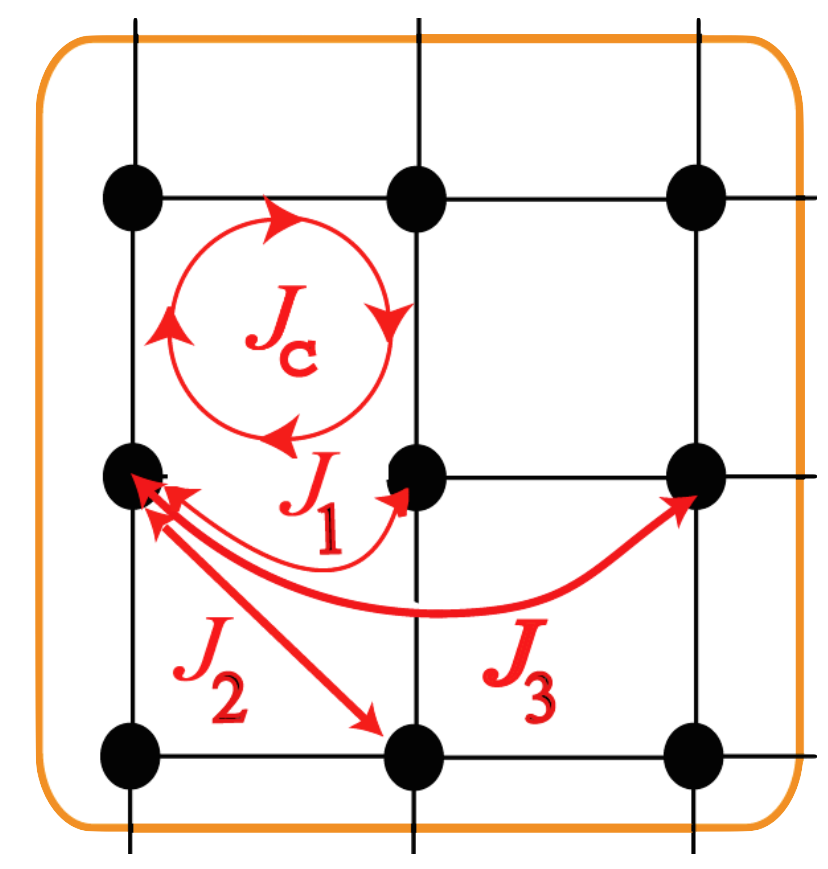
Since the discovery of exchange interactions by Heisenberg and Dirac in the late 1920s, the study of the quantum mechanical nature of magnetism has remained a topic of significant interest to condensed matter physicists. The 1987 discovery of high-temperature superconductivity in doped copper-oxide materials, such as La_2-xSr_xCuO₄, which are, surprisingly, insulating and antiferromagnetic in their undoped form (e.g. La₂CuO₄), exposed, however, our rather incomplete understanding of quantum magnetism. Some of the research pursued in my group is aimed at understanding aspects of the microscopic magnetic interactions at play in real materials. For example, we have studied how the hopping of electrons in a so-called extended Hubbard model describing La₂CuO₄ generates pairwise superexchange spin-spin interactions of various range and various types of multiple-spin couplings called ring exchange. The figure to the left illustrates how pairwise superexchanges (J₁, J₂, J₃) couple spins to different distances and how ring-exchange, J_c, couples together the four spins that form an elementary square plaquette (Delannoy et al., Phys. Rev. B 79, 235130 [2009]). We are currently working at determining similar exchange interactions for extended Hubbard models on other lattice architectures such as the anisotropic triangular lattice, a system that is attracting much attention for its realization in the quasi two-dimensional organic compounds proposed as candidates for a quantum spin liquid state. We are also studying the problem of magnon Hall effect in the Lu₂V₂O₇ pyrochlore material in collaboration with density-functional theory (DFT) experts and neutron scattering experimentalists.

Frustration, arising from competing interactions, is common in condensed matter systems. Frustration is at play in the phenomenon of protein folding and is believed to be responsible for the exotic structure of the nuclear matter, called nuclear pasta, in the interior of neutron stars. Frustration is also at play in common water ice in which the oxygen ions form a regular lattice, but where the hydrogen bonds from the proton between each water molecule is in strong competition with each other. As a compromise, the protons obey a so-called ice rule: for each oxygen ion, two protons are closed and covalently bonded to it, and two are far and hydrogen bonded to it. As a result, the protons in water ice do not form a regular crystalline structure, but are partially random.

Frustration can also occur in magnetic systems. It arises either from the competition between spin-spin interactions of different nature or different spatial range, or can be induced by the lattice structure (e.g. triangular, face-centered cubic, etc.) for interactions that are antiferromagnetic and solely acting between nearest-neighbour spins. Magnetic materials are often amenable to precise microscopic modeling and can be experimentally studied by a gamut of techniques spanning an enormously wide range of time and length scales. Because of that, it is generally believed that the study of frustrated magnetic systems may allow condensed matter physicists to unravel in a most efficient manner the generic principles that govern collective behaviour among vast classes of frustrated condensed matter systems.

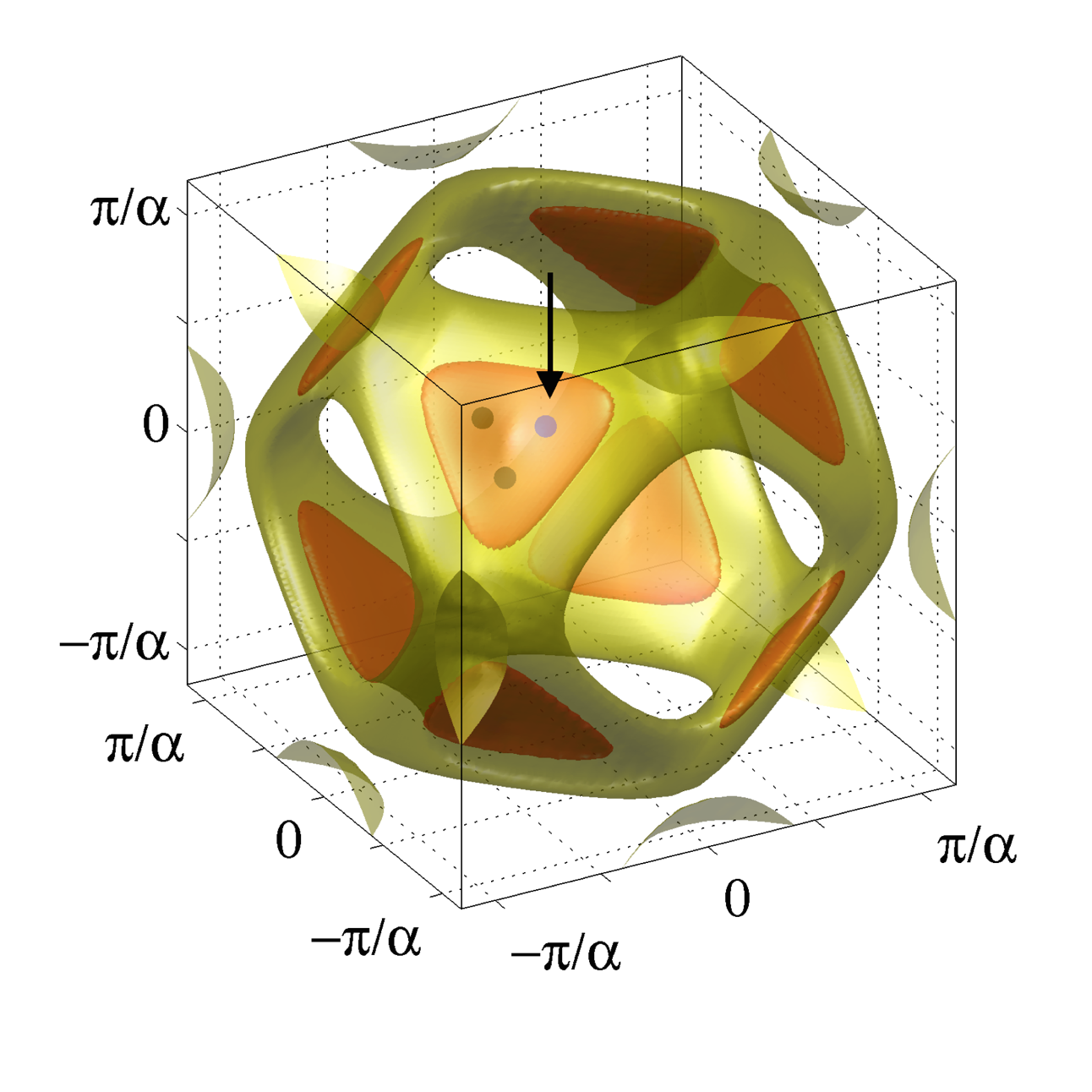
My group has been active for many years investigating phenomena in models of magnetic systems, often collaborating with experimental groups. The figure to the side illustrates the spectrum of quasi-degenerate soft (critical) modes in the Gd₃Ga₅O₁₂ garnet (referred to as GGG). These soft modes determine the periodicity (wavevector) for the orientation of the magnetic moment that spontaneously develops at the critical temperature. In a conventional/non-frustrated magnet, the soft-mode spectrum is sharply peaked at a single wavevector in the Brillouin zone. In highly frustrated magnets, the spectrum is often very diffuse and extended. This is a manifestation (in reciprocal space) of the strong frustration among the underlying magnetic interactions of a system. An interesting phenomenon that can occur in a frustrated magnetic system is order-by-disorder in which the system orders in a state in which it fluctuates, either thermally or quantum mechanically, the most among a large number of classically degenerate states. My group has recently carried out a number of projects on this topic, in particular in the context that order-by-disorder may be at play in the Er₂Ti₂O₇ frustrated antiferromagnet (Oitmaa et al., Phys. Rev. B 88, 220404 [2013]; Wong, Hao and Gingras, Phys. Rev. B 88, 144402 (2013); McClarty, Stasiak and Gingras, Phys. Rev. B 89, 024425 [2014]). At the present time, we are busy trying to construct an effective quantum spin-1/2 theory explaining the peculiar properties of the frustrated Tb₂Ti₂O₇ material, a system that has kept researchers in the field bemused for over fifteen years.

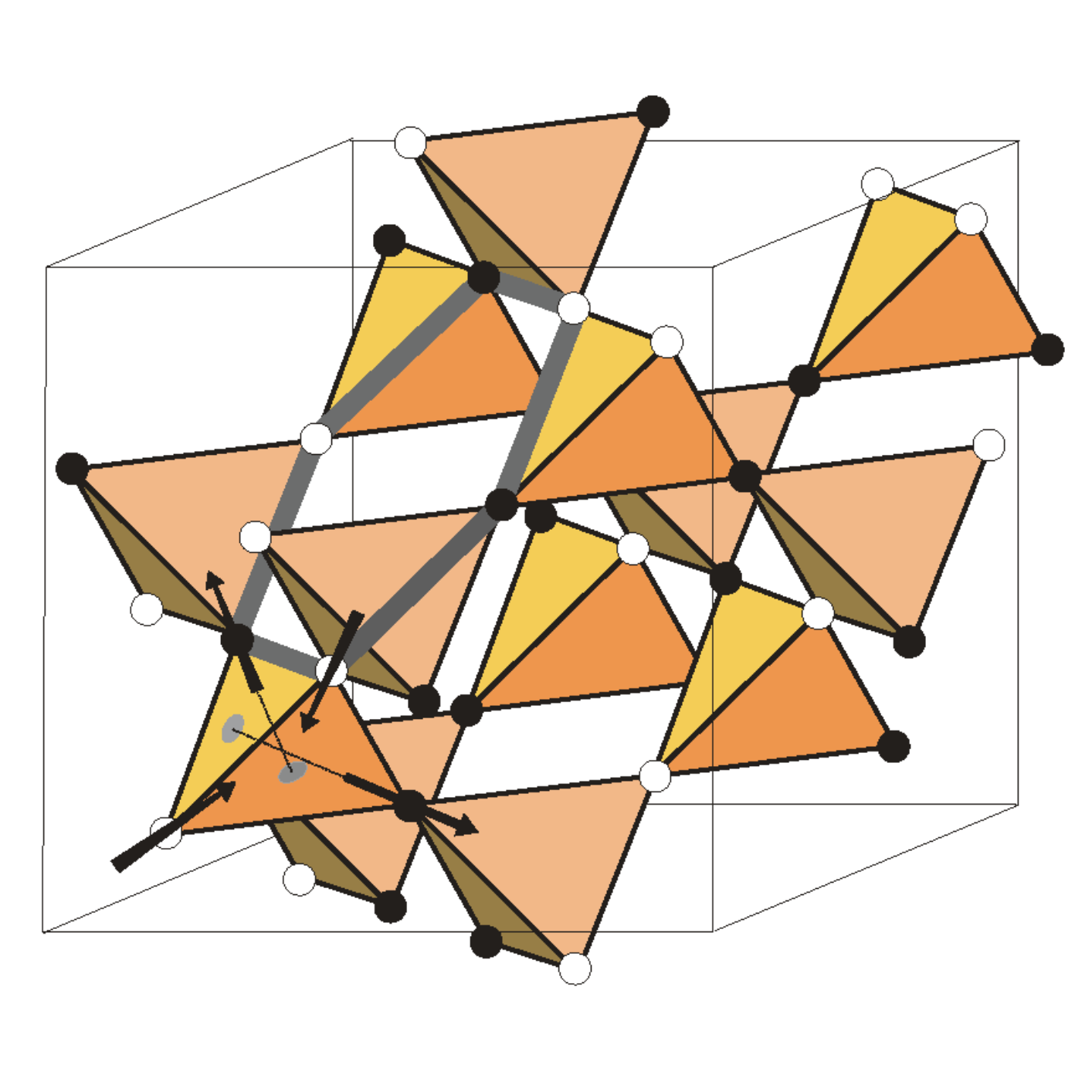
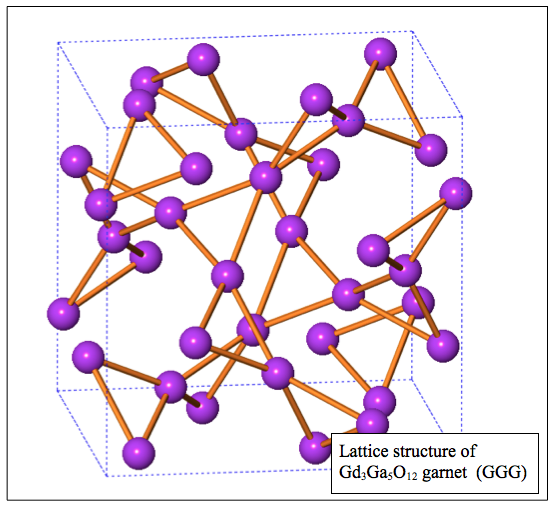
Spin ices are frustrated magnetic systems, so they could have been included in the paragraph above. However, they have been so extensively studied worldwide and by my group since their discovery in 1999 that they deserve their own discussion as they are truly fascinating. The magnetic moments in these systems reside on the vertices of a lattice of corner-sharing tetrahedra (illustrated by the white and black sites in the figure beside). The magnetic interactions between the Ho and Dy magnetic ions, in the predominantly classical (i.e. where quantum effects are negligible) Ho₂Ti₂O₇ and Dy₂Ti₂O₇ compounds, are frustrated and a low-energy state is reached when there are two magnetic moments pointing “in” and two magnetic moments pointing “out” on each tetrahedron, as shown in the bottom left tetrahedron in the figure. This can be equivalently represented with two black sites and two white sites on each tetrahedron. This low-energy rule is akin to that of the proton binding in common water ice discussed above, hence the name spin ice. The following are a few reviews on the topic Bramwell and Gingras, Science 294, 1495 [2001]; Gardner, Gingras and Greedan, Rev. Mod. Phys. 82, 53 [2010]; Gingras, Physics in Canada, 68.2, [2012].

Perhaps one of the most interesting theoretical aspects of these systems is their field theory description being akin to Gauss’ law of electrostatic. In this theory, the violation of the “two-in/two-out” rule via the thermal excitation (flipping) of a magnetic moment can be described by effective “monopole” charges that interact with each other via an emerging magnetic 1/r Coulomb potential. Experimentalists in the field are now busy searching for materials that would be a quantum variant of spin ice or quantum spin ice (Gingras and McClarty, Reports Progress in Physics 77, 056501 [2014]), in which the spins can now quantum mechanically fluctuate unlike the strictly thermal fluctuations experienced by the so-far studied classical Ho₂Ti₂O₇ and Dy₂Ti₂O₇ spin ices. Quantum spin ices are expected to be particularly interesting for being described by a quantum field theory akin to that of quantum electrodynamics (QED) on the lattice, displaying gapped “electric” and “magnetic” field charges along with an emergent gauge boson, or “artificial photon”, as low-energy excitations. My group is currently investigating various aspects of the theory of quantum spin ices (such as a recent bosonic many-body theory of these systems, Hao, Day and Gingras, Phys. Rev. B 90, 214430 [2014]) and finding ways to make connections between theory and experiments (Applegate et al. Phys. Rev. Lett. 109, 097205 [2012]).

All real materials contain some form of “frozen-in” disorder. It may be crystalline defects, such as dislocations or vacancies, or it may be chemical impurities. Understanding the equilibrium and non-equilibrium properties of condensed matter systems with random disorder has been a focus of research in condensed matter physics since the mid 1970s. In some cases, the random disorder leads to effective random fields acting on the degrees of freedom or randomly frustrated interactions. In the latter case, the system may develop a glass state at sufficiently low temperature. The theory of random disordered systems is quite difficult and is still not fully developed with many problems remaining open. In part for that reason, large-scale computer simulations have played a very important role in guiding the physicists’ understanding of these systems. Even then, standard numerical methods for systems without random disorder are often inadequate to tackle the key questions at stake. In that case, new algorithms must be developed from scratch. I have had interests in random-disordered condensed matter systems for a number of years and my group has studied the effects of random disorder in molecular, superconducting and magnetic systems, including the development of new algorithms to find the numerically exact ground state of magnetic (spin) glasses with continuous symmetry (Weigel and Gingras, Phys. Rev. Lett. 96, 097206 [2006]).

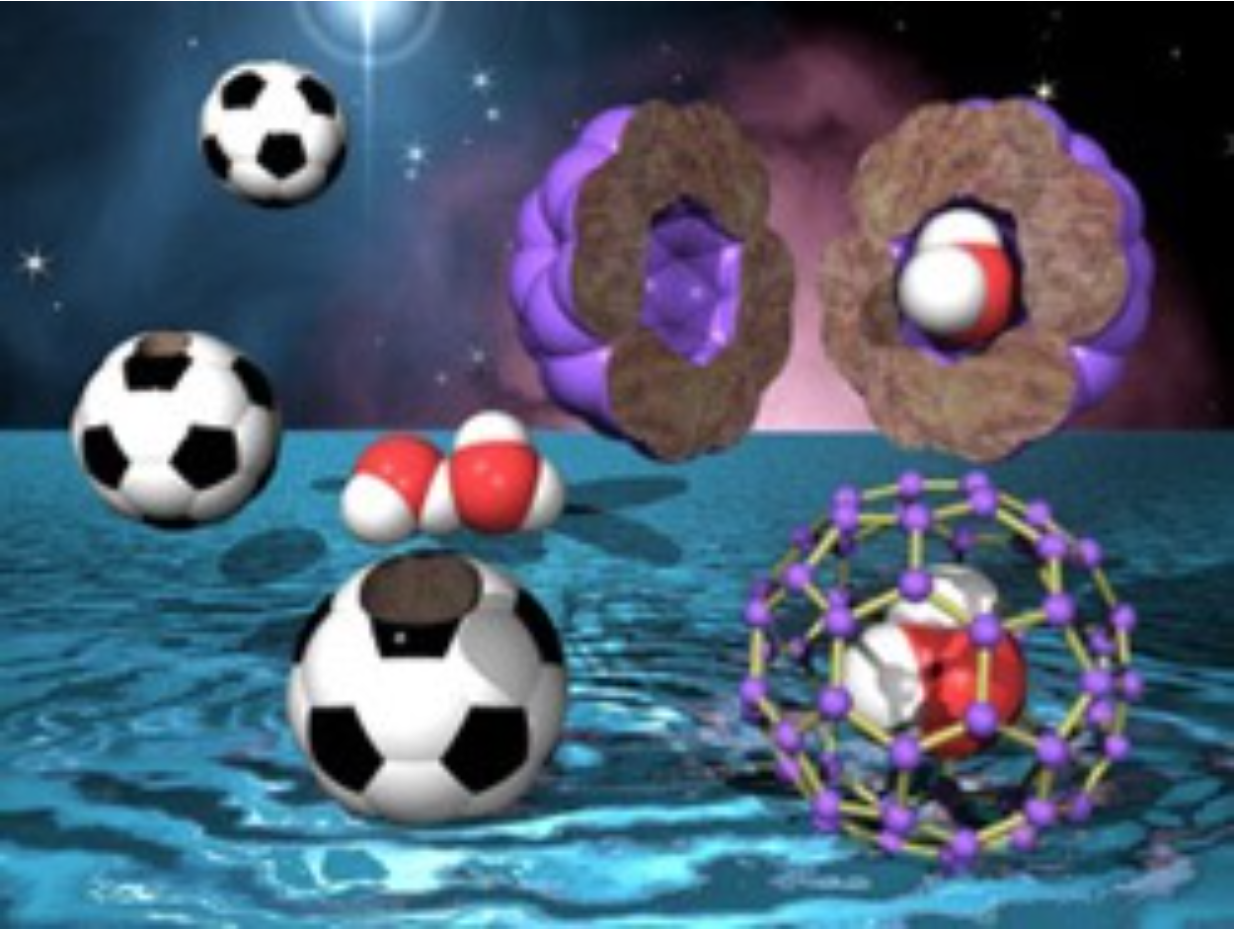
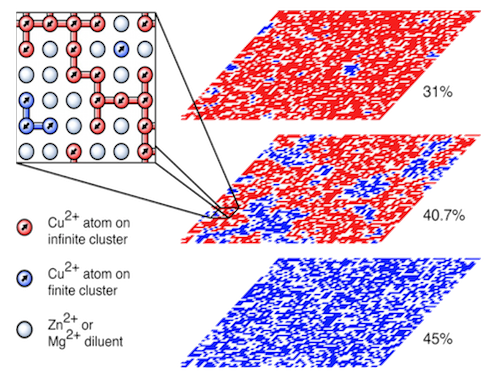
Another problem that we have studied is how quantum mechanical zero-point magnetic fluctuations depend on the site-dilution of the magnetic moments in a system such as La₂Cu_1-yZn_yO₄ in which non-magnetic Zn²⁺ ions randomly replace the magnetic Cu²⁺ spin-1/2 ions as illustrated in the figure above (Delannoy et al., Phys. Rev. B 79, 224414 [2009]). Most recently, we joined forces with an experimental group to investigate how the dilution of the magnetic moments by non-magnetic ions in spin ice materials affect the “two-in/two-out” ice rules (Lin et al., Phys. Rev. B 90, 214433 [2014]). It has recently become possible to embed water molecules in the interior of C₆₀ buckminsterfullerene molecules (see figure to the left). A project that we are currently exploring is how the incomplete occupation of water molecules in crystals of C₆₀ affects their collective molecular orientational behaviour and, in particular, the dielectric properties of this unusual system.